FPS矩阵原理

参考文章： FPS通用的方框透视公式的原理_fps透视原理-CSDN博客

​ FPS游戏方框透视基本原理_fps 透视矩阵算法-CSDN博客

之前我们做的非矩阵画线，位置不准确，还很难进行缩放

但是下图是矩阵的效果，看上去就非常的好

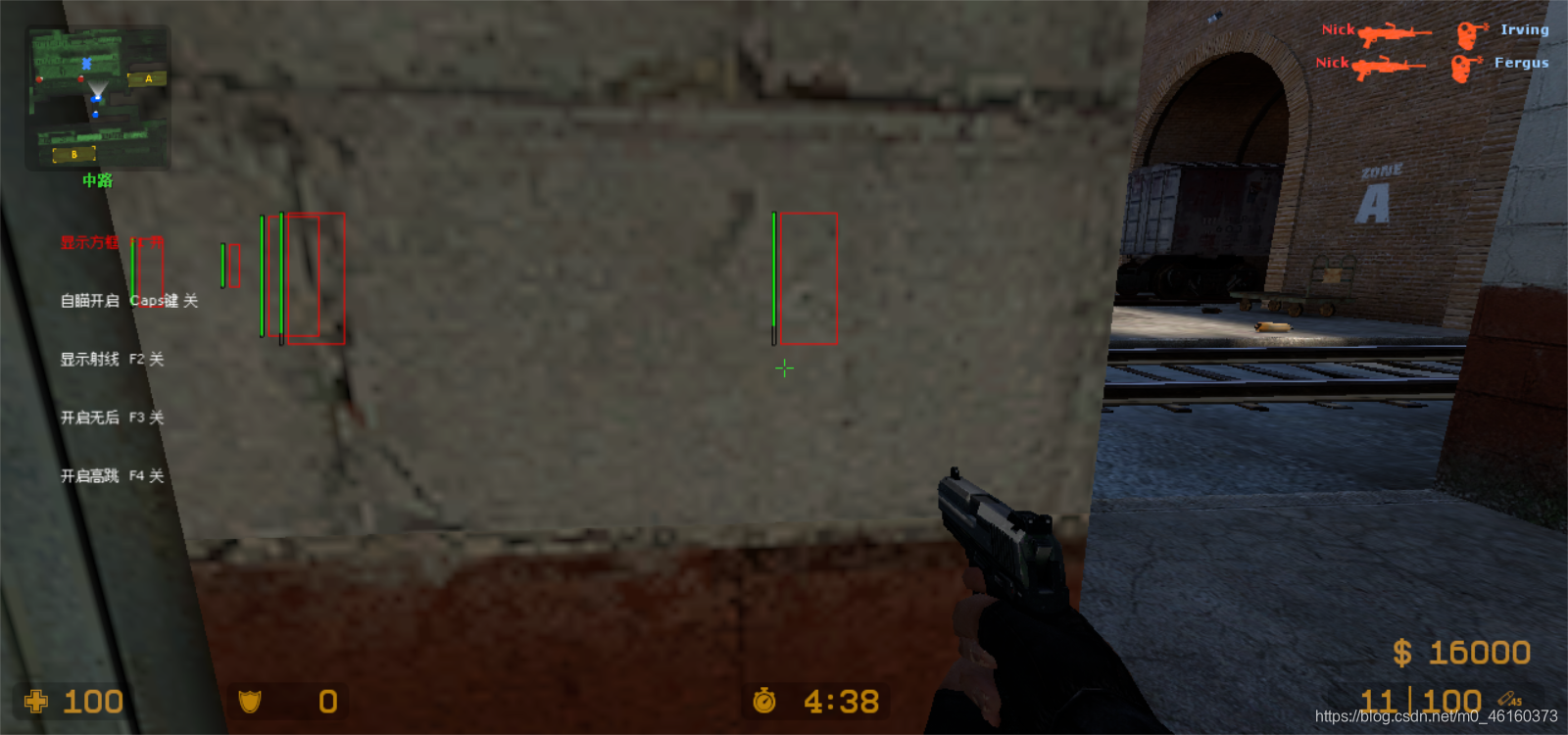
1723452172962

游戏坐标转换原理：

游戏中通过建模完成的3D物体要想在2D屏幕上显示出来需要进行坐标的转换。

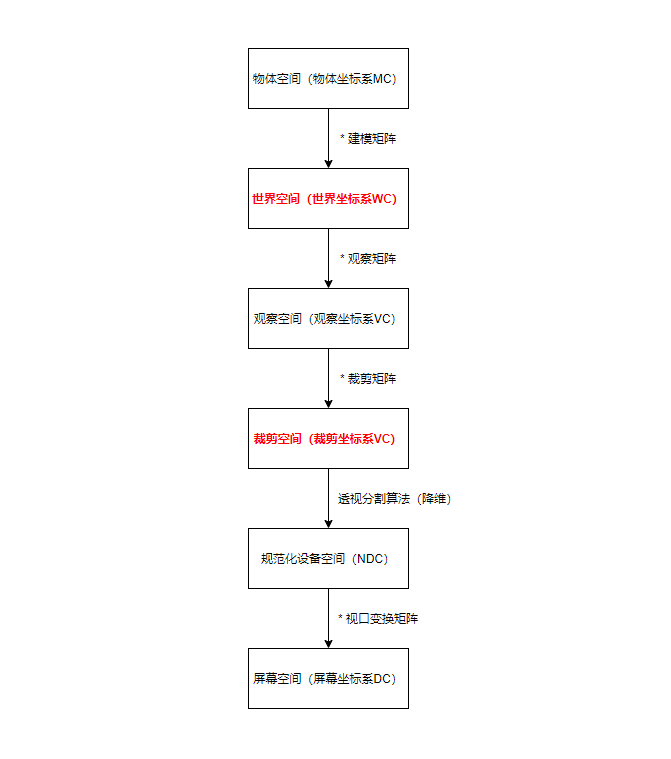
1723452889917

具体过程看 FPS游戏方框透视基本原理_fps 透视矩阵算法-CSDN博客 吧（看得我十分头大，不过我们只需要大概了解即可）

按照上面的原理，我们只要找到人物在世界坐标系中的坐标 （x1，y1，z1） ，就可以在屏幕上画出人物边框

第一步：世界坐标 -> 裁剪坐标

z1后面的那个1是w，为了兼容4*4矩阵

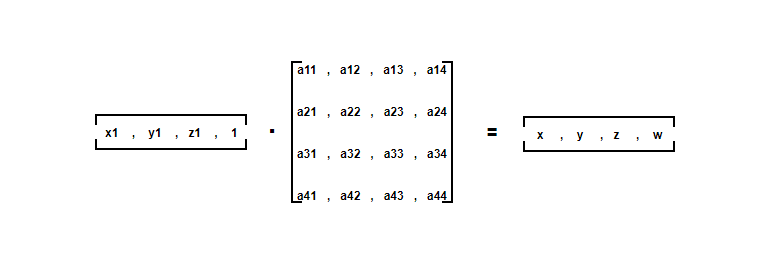
1723453200617

1
2
3
4
5
6
7
8
9
10
X = a11*x1 + a12*y1 + a13*z1 + a14
 
Y = a21*x1 + a22*y1 + a23*z1 + a24
 
Z = a31*x1 + a32*y1 + a33*z1 + a34
 
W = a41*x1 + a42*y1 + a43*z1 + a44
 
//(x, y, z)就是（x1，y1，z1）对应的裁剪坐标
//注意w有可能小于0，如果w小于说明物体不在你的视角范围中（不需要在屏幕上显示）。

裁剪坐标 —-> NDC坐标

NDC坐标就是将裁剪坐标对应的xyz除以w，这就是透视分割算法（降维）。 

1
2
3
NDC_X = X / W
 
NDC_Y = Y / W

NDC坐标 —-> 屏幕坐标

这需要一个视口变换矩阵，视口变换矩阵左乘NDC坐标就会得到对应的屏幕坐标。其中视口变换矩阵中fs和ns一般为0。

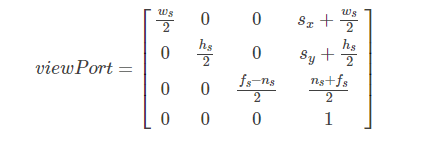
1723453359667

最后得到屏幕坐标的X = (Ws / 2 * NDC.x) + (NDC.x + Ws / 2)， Y = -(Hs / 2 * NDC.y) + (NDC.y + Hs / 2)。而Ws * Hs为当前屏幕窗口的分辨率，且注意在windows中屏幕坐标系的规则

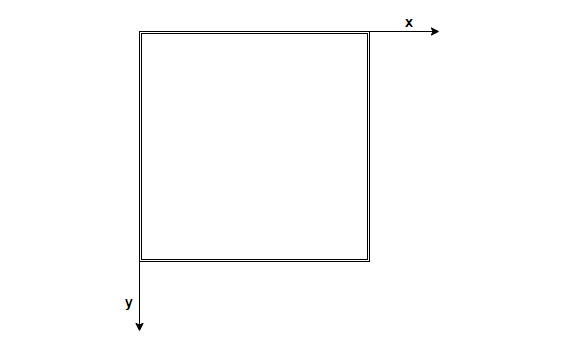
1723453379859

我们需要找什么矩阵

在开发FPS游戏的辅助工具（俗称“外挂”）时，“找矩阵”通常指的是找到与游戏中物体或玩家视角相关的变换矩阵。这些矩阵可以是Direct3D（D3D）或OpenGL中用于渲染场景的矩阵。

D3D矩阵和OpenGL矩阵 包括了用于计算相机视角的所有变换矩阵：

世界矩阵（World Matrix）：将物体从局部坐标系转换到世界坐标系。

视图矩阵（View Matrix）：将世界坐标系转换到相机坐标系。

投影矩阵（Projection Matrix）：将相机坐标系转换到屏幕坐标系，并决定了FOV。

其实我们要找的就是相机FOV的矩阵，然后这个矩阵是通过D3D矩阵或openGL矩阵将一个坐标矩阵变换而来，最终得到一个相机FOV的矩阵

其中：
D3D矩阵 是行主序

1
2
3
4
5
6
a00,   a01,  a02,  a03,                      

a10,   a11,  a12,  a13,  

a20,   a21,  a22,  a23,                                        
a30,   a31,  a32,  a33,  //行主序

openGL矩阵 是列主序

1
2
3
4
5
6
a00,   a10,  a20,  a30,

a01,   a11,  a21,  a31,

a02,   a12,  a22,  a32,                                  
a03,   a13,  a23,  a33,  //列主序

介绍找到的矩阵特性：

缩放和位移矩阵：

1
2
3
4
Sx 0 0 Tx
0 Sy 0 Ty
0 0 Sz Tz
0 0  0 Tw

这样，一个坐标矩阵
(
x
y
z
w
）

乘上这个坐标矩阵之后就会得到

(
Sx * x + Tx * w
Sy * y + Ty * w
Sz * z + Tz * w
Tw*w
）

)

缩小放大S倍，移动就用T * w表示

在FPS游戏中，角色的运动如走路、跳跃等，实际上会引起摄像机视点的变化。这个变化体现在位置的变换上，而位置的变换就体现在矩阵的最后一列。

结论1

所以得出结论：
行主序的最后一列，列主序的最后一行，在走路 跳的时候会改变（不代表其他动作不改变）

注意注意，貌似单纯跳，直走之后改变三个值，但是如果混合运动，就会四个值一起改变，这个也可以作为特征

旋转矩阵：

注意一下，以下说的xyz轴，都是以人物建立坐标系，不是世界坐标系

这是在xyz坐标系中的xy平面进行旋转，也就是绕着z轴旋转

1
2
3
4
cosA	-sinA	0	0
sinA	cosA	0	0
0		0		1	0
0		0		0	1

乘上 坐标列矩阵
(
x
y
z
w
) （右乘）

可以得到：

(
cosA * x - sinA * y
sinA * x +cosA * y
z
w

)

例如下面的转换

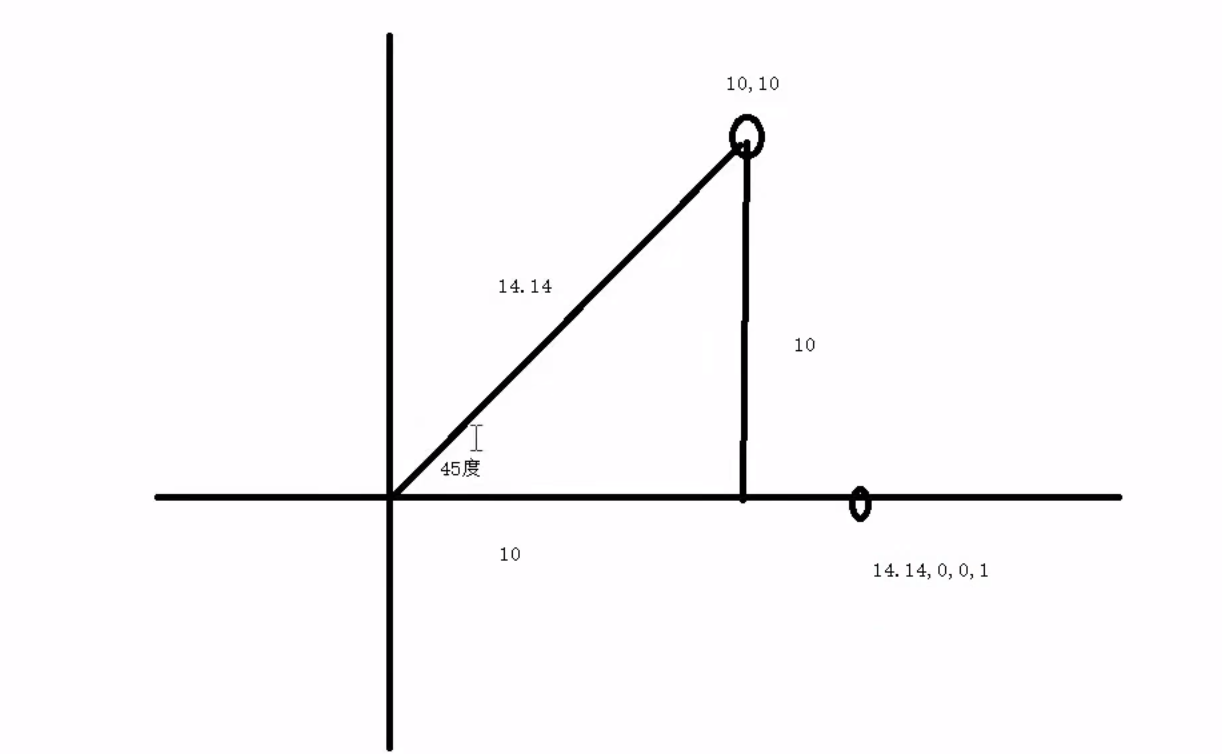
1723460972563

同理还有绕着x轴，y轴旋转

那么旋转矩阵就变为

1
2
3
4
5
6
7
8
9
10
11
//绕x轴旋转
1	0	0	0
0 cosA -sinA 0
0 sinA cosA 0
0	0	0	1
    
//绕y轴旋转
cosA  0  sinA  0
0	  1   0    0
-sinA 0  cosA  0
0     0   0    1

结论2

因此我们又得出一个结论：

在水平转动的情况下，也就是绕着Z轴旋转，行主序的第三列不变，列主序的第三行不变

同理

结论3：

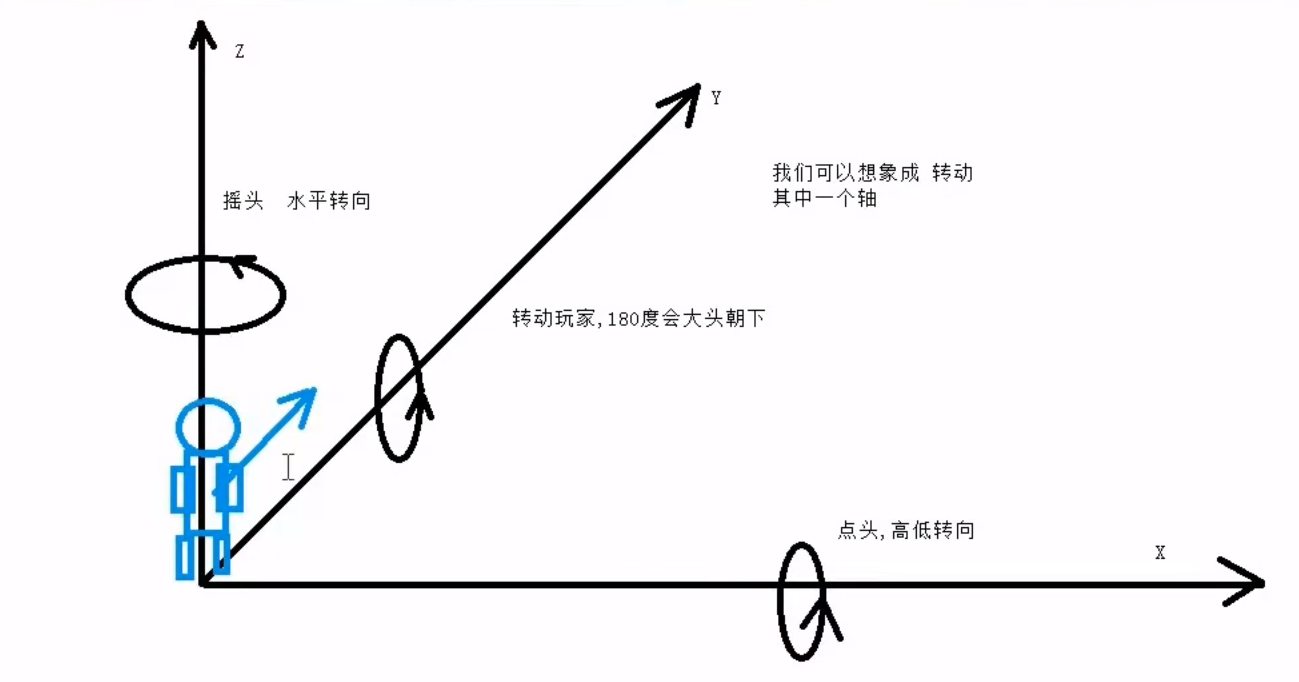
1723474315591

在高低朝向改变的时候，其实就是绕着x轴进行旋转

所以结论：

高低朝向改变的时候，行主序的第一行不变，列主序的第一列不变

其他结论：

很多的FPS游戏的规律：矩阵4*4的第一个值是-1到1,这是和引擎的特性有关（不一定）

行主序的第一行第三个元素是固定的0，列主序的第一列的第三个元素是0 （可能也不一定）

开倍镜的情况下，矩阵4*4的第一个值会乘相应的倍数（大概率对）

合集：

  1. 行主序的最后一列，列主序的最后一行，在走路 跳的时候会改变（不代表其他动作不改变）
  2. 在水平转动的情况下，也就是绕着Z轴旋转，行主序的第三列不变，列主序的第三行不变
  3. 高低朝向改变的时候，行主序的第一行不变，列主序的第一列不变
  4. 很多的FPS游戏的规律：矩阵4*4的第一个值是-1到1,这是和引擎的特性有关（不一定）
  5. 行主序的第一行第三个元素是固定的0，列主序的第一列的第三个元素是0 （可能也不一定）
  6. 开倍镜的情况下，矩阵4*4的第一个值会乘相应的倍数（大概率对）

找矩阵实践：

先说结论：

1
cstrike.exe+1820100  //矩阵基地址

其实就是应用上述的结论，主要是结论1 结论2 结论3和最后一个开镜矩阵的第一个值会放大

值得注意的是，一开始我咋也找不着，因为我直接根据开镜第一个值就变大，不开镜就变小的结论去找

但是我忽略了一点，就是第一个值有可能是一个负数，这样开镜的话，乘以一个倍数就会变得更小，但是我仍然按照增大的值去搜，导致一无所获，这也算是学了个教训吧

还有其他技巧，就是原地跳，那么结论1的第一个值是不会变的，还有改朝向，只要是人物朝向和世界坐标的x y轴重合，那么直走的时候，结论1的第一个值也是不会变的

坐标转换：

世界坐标->剪辑坐标

拿世界坐标矩阵

1
x	y	z	w

去乘以我们刚刚找到的矩阵

1
2
3
4
5
6
7
8
9
10
11
a0	a1	a2	a3
a4	a5	a6	a7
a8	a9	a10	a11
a12	a13	a14	a15
    
    
也有可能是列主序
a0	a4	a8	a12
a1	a5	a9	a13
a2	a6	a10	a14
a3	a7	a11	a15

得到结果：

1
2
3
4
5
6
7
8
9
10
剪辑坐标x=a0*x+a4*y+a8*z+a12*w
剪辑坐标y=a1*x+a5*y+a9*z+a13*w
剪辑坐标z=a2*x+a6*y+a10*z+a14*w
剪辑坐标w=a3*x+a7*y+a11*z+a15*w
    

剪辑坐标x=a0*x+a1*y+a2*z+a3*w
剪辑坐标y=a4*x+a5*y+a6*z+a7*w
剪辑坐标z=a8*x+a9*y+a10*z+a11*w
剪辑坐标w=a12*x+a13*y+a14*z+a15*w

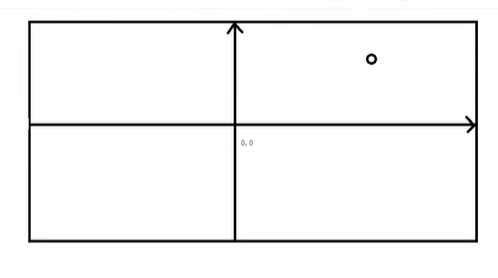
1723551364606

此时将世界坐标转换为了二维平面的坐标，但是和设备的分辨率没啥关系，需要进一步变换

剪辑坐标->NDC坐标：

1
2
3
NDC.x = 剪辑坐标x/剪辑坐标w
NDC.y = 剪辑坐标y/剪辑坐标w
NDC.z = 剪辑坐标z/剪辑坐标w

把剪辑坐标变成范围限定在-1~1

NDC坐标->屏幕坐标：

1
2
NDC.x/1=屏幕坐标差.x / （分辨率_宽/2）
NDC.y/1=屏幕坐标差.y / （分辨率_高/2）

所以我们可以推出来：

1
2
3
4
5
屏幕坐标.x = 屏幕坐标差.x + 分辨率_宽/2
    		(分辨率_宽/2)*NDC.x + 分辨率_宽/2
    
屏幕坐标.y = -屏幕坐标差.y + 分辨率_高/2   
    		-(分辨率_高/2)*NDC.y + 分辨率_高/2

额外加一个 分辨率 _ 宽/ 2 ， 分辨率_高/2 是因为NDC坐标原点在屏幕中心

还有在NDC坐标系中，一二象限的y是正值，三四象限是负值，但是我们的屏幕坐标从上到下是增加的。所以我们需要自己加一个负号

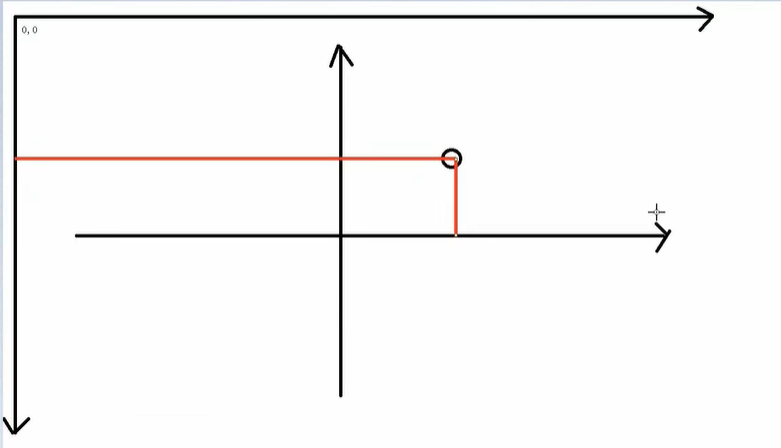
1723551616311

世界坐标转为屏幕坐标代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
bool 绘制::世界坐标转为屏幕坐标_矩阵(对象结构 目标对象结构, 屏幕坐标结构& 目标屏幕坐标结构)
{
	for (int i = 0; i < 16; i++)
	{
		矩阵[i] = *(float*)(矩阵地址 + 4 * i);
	}
	DWORD w = 1;
	float 剪辑坐标x = this->矩阵[0] * 目标对象结构.对象重心的x坐标 + this->矩阵[4] * 目标对象结构.对象重心的y坐标 + this->矩阵[8] * 目标对象结构.对象重心的z坐标 + this->矩阵[12] * w;
	float 剪辑坐标y = this->矩阵[1] * 目标对象结构.对象重心的x坐标 + this->矩阵[5] * 目标对象结构.对象重心的y坐标 + this->矩阵[9] * 目标对象结构.对象重心的z坐标 + this->矩阵[13] * w;
	float 剪辑坐标z = this->矩阵[2] * 目标对象结构.对象重心的x坐标 + this->矩阵[6] * 目标对象结构.对象重心的y坐标 + this->矩阵[10] * 目标对象结构.对象重心的z坐标 + this->矩阵[14] * w;
	float 剪辑坐标w = this->矩阵[3] * 目标对象结构.对象重心的x坐标 + this->矩阵[7] * 目标对象结构.对象重心的y坐标 + this->矩阵[11] * 目标对象结构.对象重心的z坐标 + this->矩阵[15] * w;

	if (剪辑坐标w < 0.0f)
	{
		目标屏幕坐标结构.x坐标 = 分辨率_宽 / 2;
		目标屏幕坐标结构.y坐标 = 分辨率_高 * 3 / 4;
		return false;
	}


	float NDC_x = 剪辑坐标x / 剪辑坐标w;
	float NDC_y = 剪辑坐标y / 剪辑坐标w;

	目标屏幕坐标结构.x坐标 = (分辨率_宽 / 2) * NDC_x + 分辨率_宽 / 2;
	目标屏幕坐标结构.y坐标 =  0-(分辨率_高 / 2) * NDC_y + 分辨率_高 / 2;
	return true;
}